Let us consider the equation  in which  and  are both unknown. It is very clear that this equation will hold true, i.e., be satisfied for all values of  and . We can safely say that this equation has an infinite number of solutions because any pair of numbers whose difference is 2 will satisfy the equation. For example, ; ; ; and so on. However, if, together with this equation we consider the equation  then  and  must be such that their difference is 2 and their sum is 8. Thus, the two equations  will both be satisfied by the same pair of values of  and  only when  and 

Again, let us consider the following equations:

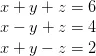
These equations will be satisfied by the same values of  only when . These equations may be individually satisfied for all values of the unknown quantities, but there is only one set of values of  which will satisfy all three equations simultaneously. Two or more equations which are all satisfied by a single set of values of the involved variables are called simultaneous equations.

Consider the two linear equations  and . Each of these two equations contains two variables (namely  and ) and together these equations are called simultaneous (linear) equations. These equations are linear simultaneous equations or simple simultaneous equations because the maximum power of the variables involved in them is 1.

Methods of Solving Simultaneous Equations

The methods for solving simultaneous equations are as follows:

·         Method of Substitution

·         Method of Elimination

·         Method of Comparison