Let us consider the equation 
in which 
and 
are both unknown. It is very clear that this equation will hold true, i.e., be satisfied for all values of and . We can safely say that this equation has an infinite number of solutions because any pair of numbers whose difference is 2 will satisfy the equation. For example, 
; 
; ; and so on. However, if, together with this equation we consider the equation then and must be such that their difference is 2 and their sum is 8. Thus, the two equations 
will both be satisfied by the same pair of values of and only when 
and 
Again, let us consider the following equations:
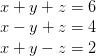
These equations will be satisfied by the same values of 
only when 
. These equations may be individually satisfied for all values of the unknown quantities, but there is only one set of values of which will satisfy all three equations simultaneously. Two or more equations which are all satisfied by a single set of values of the involved variables are called simultaneous equations.
Consider the two linear equations and . Each of these two equations contains two variables (namely and ) and together these equations are called simultaneous (linear) equations. These equations are linear simultaneous equations or simple simultaneous equations because the maximum power of the variables involved in them is 1.
Methods of Solving Simultaneous Equations
The methods for solving simultaneous equations are as follows:
· Method of Substitution
· Method of Elimination
· Method of Comparison
Comments are closed